Support Vector Machine
支持向量机(Support Vector Machines, SVM)最初由Vladimir
Vapnik于1997年提出,SVM最简单的形式就是找出一下区分界限(descision
boundary),也称之为超平面(hyperplane),使得离它最近的点(称之为support
vectors)与之间隔最大。
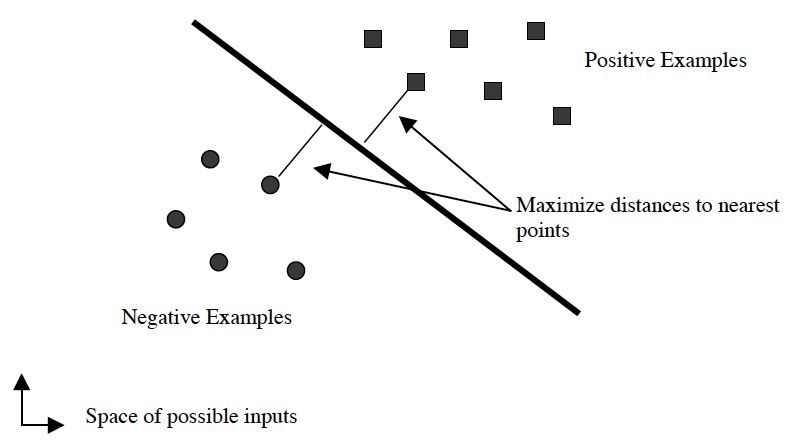
这和logistic regression有些相似,区别在于logistic regression要求所有的点尽可能地远离中间那条线,而SVM是要求最接近中间线的点尽可能地远离中间线。也就是说SVM的主要目标是区分那些最难区分的点。
SVM对于hyperplane的定义,在形式上和logistic regression一样,logistic
regression的decision boundary由$\theta^TX=0$确定,SVM则用$w^TX+b=0$表示,其中b相当于logistic regression中的$\theta_0$,从形式上看,两者并无区别,当然如前面所说,两者的目标不一样,logistic regression着眼于全局,SVM着眼于support
vectors。有监督算法都有label变量y,logistic
regression取值是{0,1},而SVM为了计算距离方便,取值为{-1,1}。
那么SVM的问题就变成为,确定参数w和b,以满足: $w^T x_i + b \ge +1$ when $y_i = +1$ $w^T x_i + b \le +1$ when $ y_i = -1$ 对于上图中最简单的例子,中间线可以由Ax+By+c=0表示,图上一个$(x_0, y_0)$的点到中间线的距离为$\frac{|Ax_0+By_0+c|}{\sqrt{A^2+B^2}}$。
对于更高维的空间,点到hyperplane上的距离也是一样计算,定义为: $\frac{|w^Tx+b|}{||w||}=\frac{1}{||w||}$。 要距离最大,也就是求||w||的最小值。 那么问题就相当于在给定条件g(x): $y_i(w^Tx_i)-b \ge 1$下,求f(x): $\frac{1}{2}||w||^2$的最大值。 这是一个限定条件下的优化问题,可以通过Lagrange multiplier解决。
这里,拉格朗日公式为: $L=\frac{1}{2}||w||^2-\sum{\alpha_i[y_i(w^Tx_i+b)-1]}$
通过对拉格朗日公式的分析,问题变为: 给定$\alpha \ge 0$ $\sum{\alpha_iy_i} = 0$ 求$\sum{\alpha_i} - \frac{1}{2}\sum{\alpha_i\alpha_jy_iy_jx_ix_j}$的最大值。
对于$\alpha$值,通常训练算法还通过C参数进行限制$C \ge \alpha \ge 0$,这个参数相当于logistic regression里的$\lambda$参数,对outlier数据点的penalty。
通过Sequential Minimal Optimization(SMO)算法,可以快速地给出解。
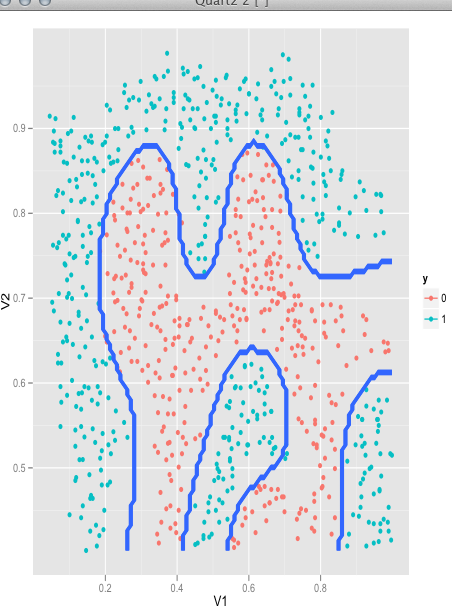
对于无法进行线性区分的数据,需要进行transformation,把数据映射到另一个空间里,使之可以线性区分,这就是kernel function所干的事情。
参考了《machine learning in action》和ml-class的材料后,我在mlass包里实现了简化版本的SMO算法。
require(mlass)
data(ex6data2)
model <- svmTrain(X,y, C=1, kernelFunction="gaussianKernel")
plot(model, X,y, type="nonlinear")