The spread of new mutations
Genetic drift is the term used in population genetics to refer to the statistical drift over time of gene frequencies in a population due to random sampling effects in the formation of successive generations. In a narrower sense, genetic drift refers to the expected population dynamics of neutral alleles (those defined as having no positive or negative impact on reproductive fitness), which are predicted to eventually become fixed at zero or 100% frequency in the absence of other mechanisms affecting allele distributions.
The most important keyword in the definition of genetic drift is random sampling effects. The figure belowed illustrates this idea. The surviving individuals do not necessarily have selection advantage. They are randomly selected.

Genetic drift can changes the proportion of genetic polymorphism. A particular mutation that are rare may becomes majority of the population due to random events. If all individuals in the population contain a particular mutation, we call it fixation.
In population genetics, fixation is the change in a gene pool from a situation where there exists at least two variants of a particular gene (allele) to a situation where only one of the alleles remains.
If there are m individuals contains a particular mutation in the population of size N, the ratio of have and do not have this mutation is $a = m/N$ , and $1-a$ respectively. According to Wright-Fisher model, the probability of n individuals that have this mutation in next generation follows the distribution of binomial: $P(n) = C^N_n a^n(1-a)^{N-n}$
With this distribution, we can perform simulation. Here, assume population size N=200, and initial probability of $ a=0.1 $ , we can sample n base on Wright-Fisher model and repeatedly update $a$ until $a$ is equals to 0 or 100%.
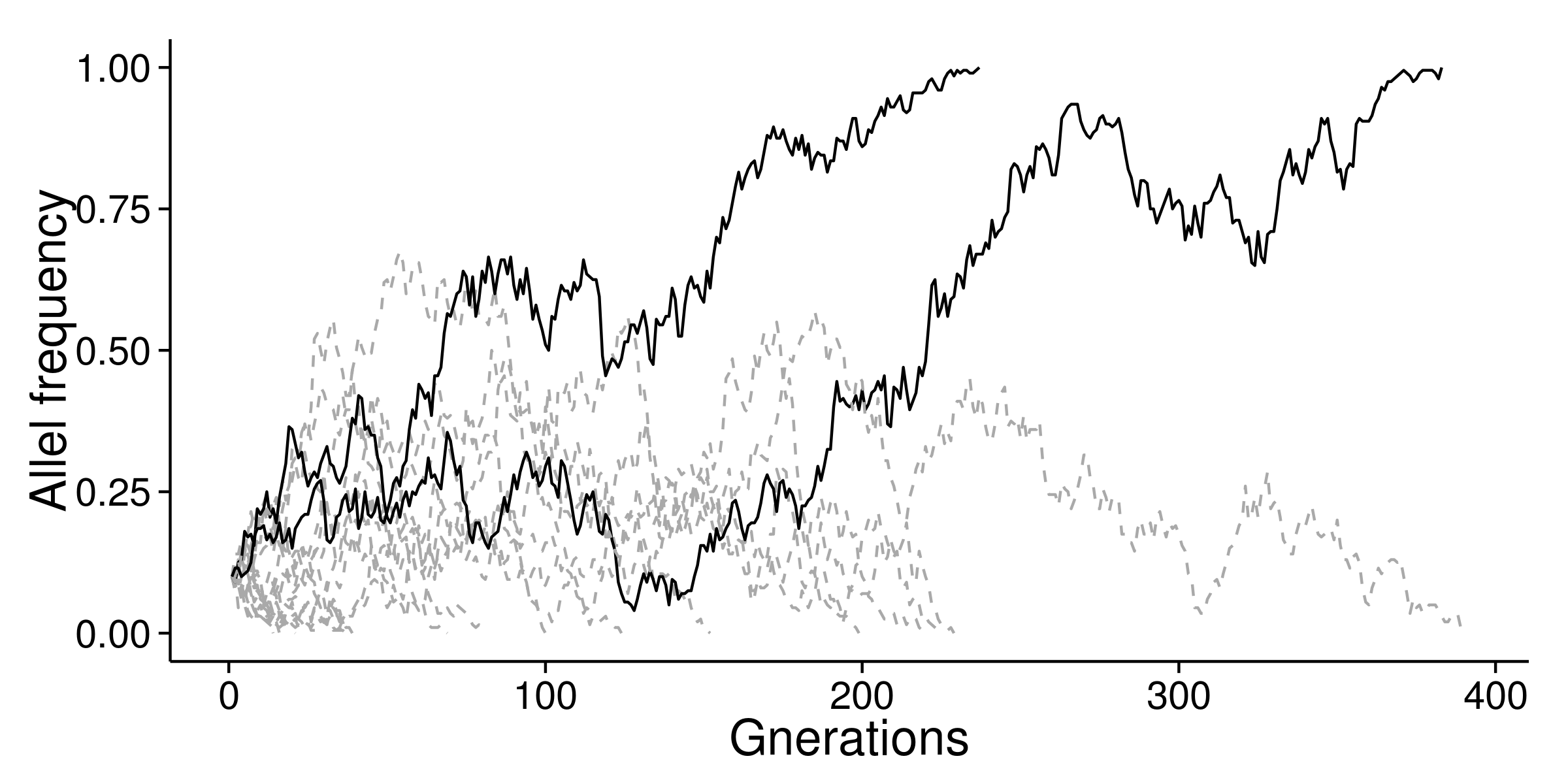
In the above figure, I showed 20 times of simulations. There are 2 fixations. The ratio 2/20 is equals to the initial value of $a$ (0.1). For neutral mutation, the probability of fixation is equals to the mutation rate.
Not all mutation are neutral. With selection pressures, some mutations have advantage while some mutations are deleterious. Advantageous mutation has fitness 1+s, while s is the selection coefficient. Fitness is the ratio between actual number of offspring and the expected offspring number. So individuals that contain advantageous mutation produce 1+s times of offspring than those do not have that mutation.
The mean of fitness in m copies of mutation is: $\bar{w} = \frac{m(1+s) + (N-m)}{N}$
In next generation, the ratio of this mutation is: $ a = \frac{m(1+s)}{N\bar{w}} $
I used s=0.05 to perform simulation again. Most of the advantageous mutation can be fixed after 100 generations.
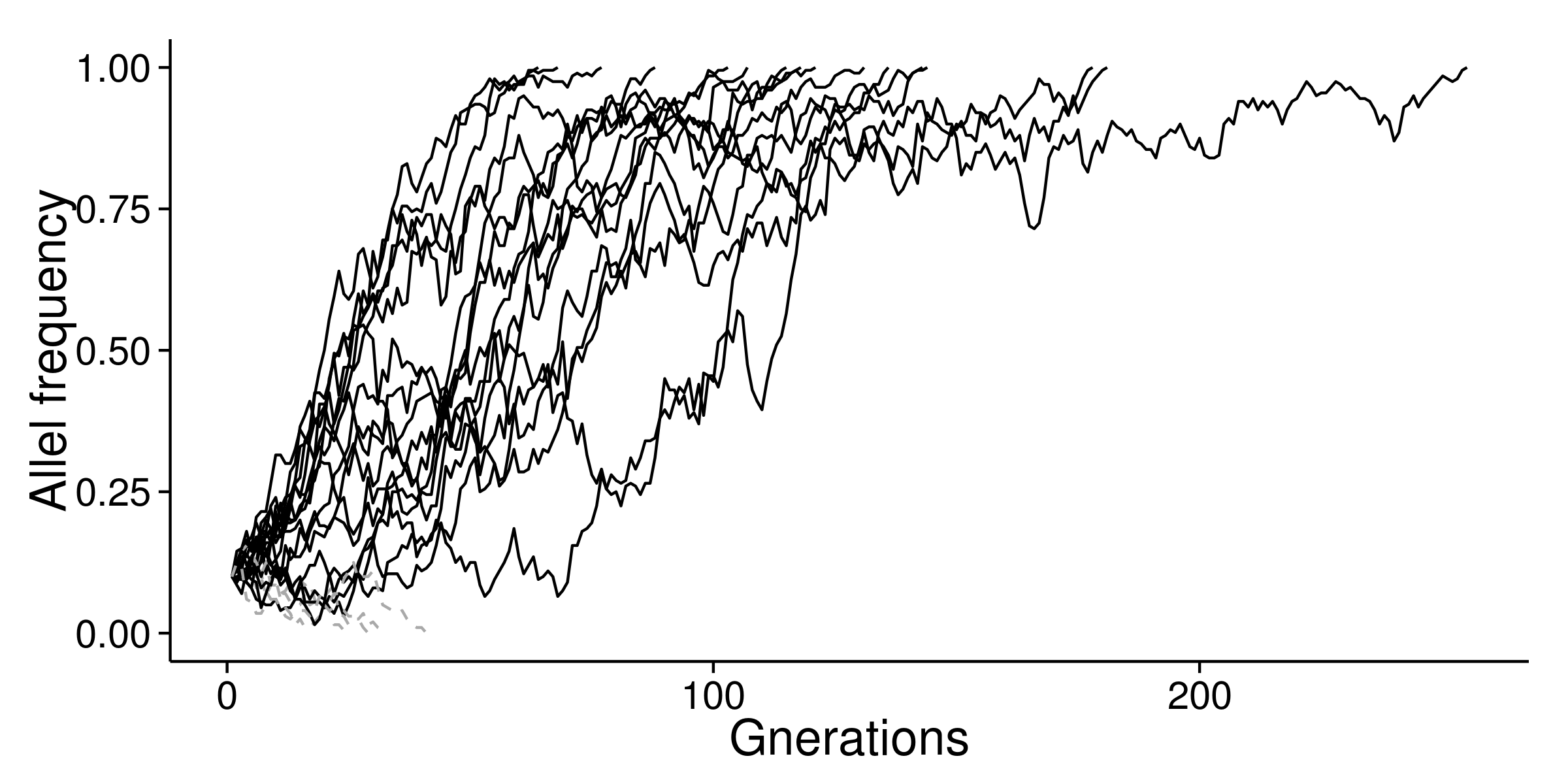
If I set s=0.2, mutation can be fixed after 30 generations.
Accordingly, if mutation is deleterious, the fitness is 1-s.
Kimura proposed diffusion theory that the probability of fixation for advantageous mutation is: $p_{fix} = \frac{1-e^{-2s}}{1-e^{-2Ns}}$
and for deleterious mutation is: $ p_{fix} = \frac{e^{2s}-1}{e^{2Ns}-1}$
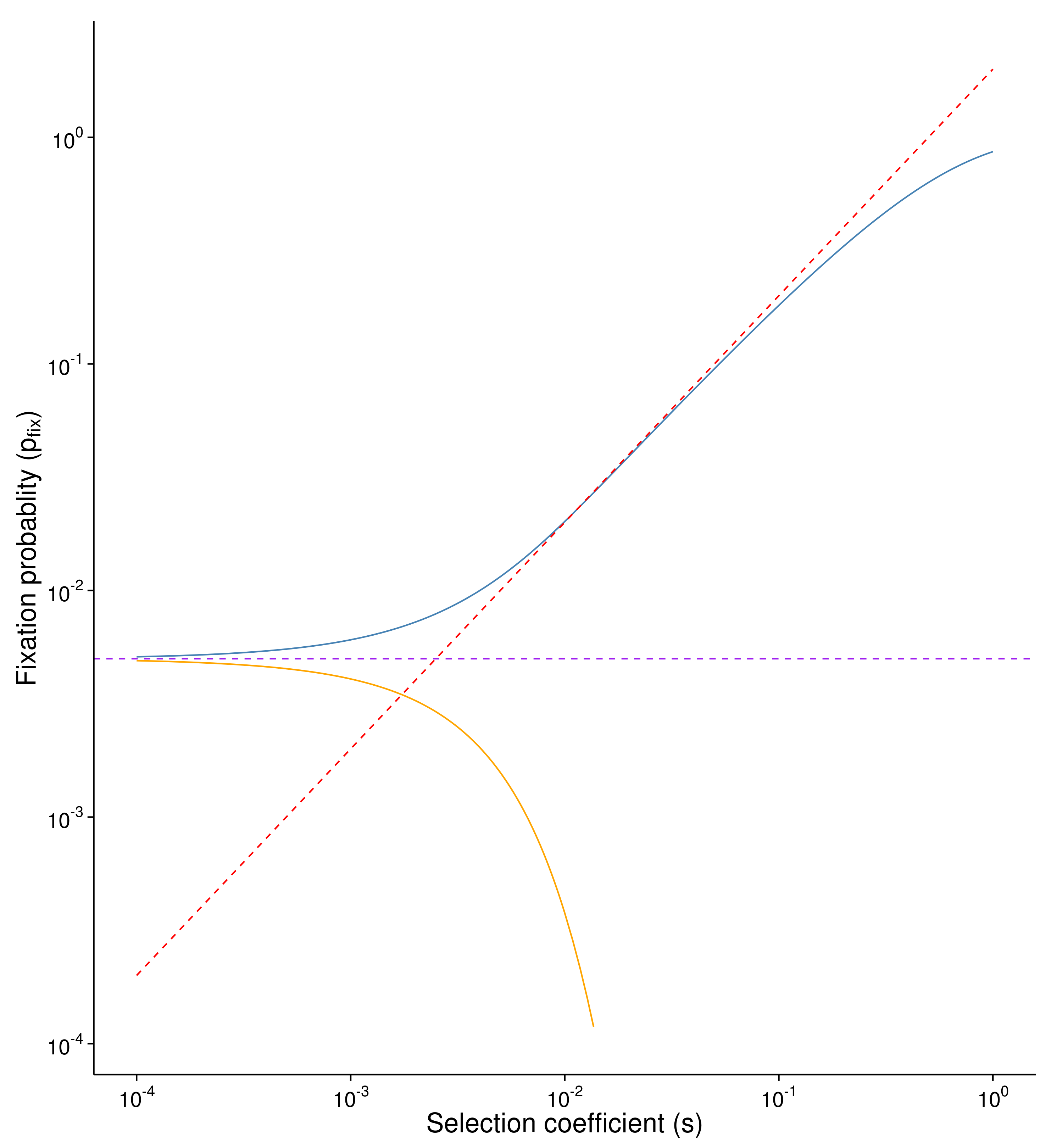
If s is very small and Ns « 1, the major force behind fixation is genetic drift, similar to neutral mutation (purple line).
In the condition of Ns » 1 and s « 1, $ e^{-2s} \approx 1-2s$ and $p_{fix} \approx 2s $ (red line).
Reference:
Chapter 3 of Bioinformatics and Molecular Evolution