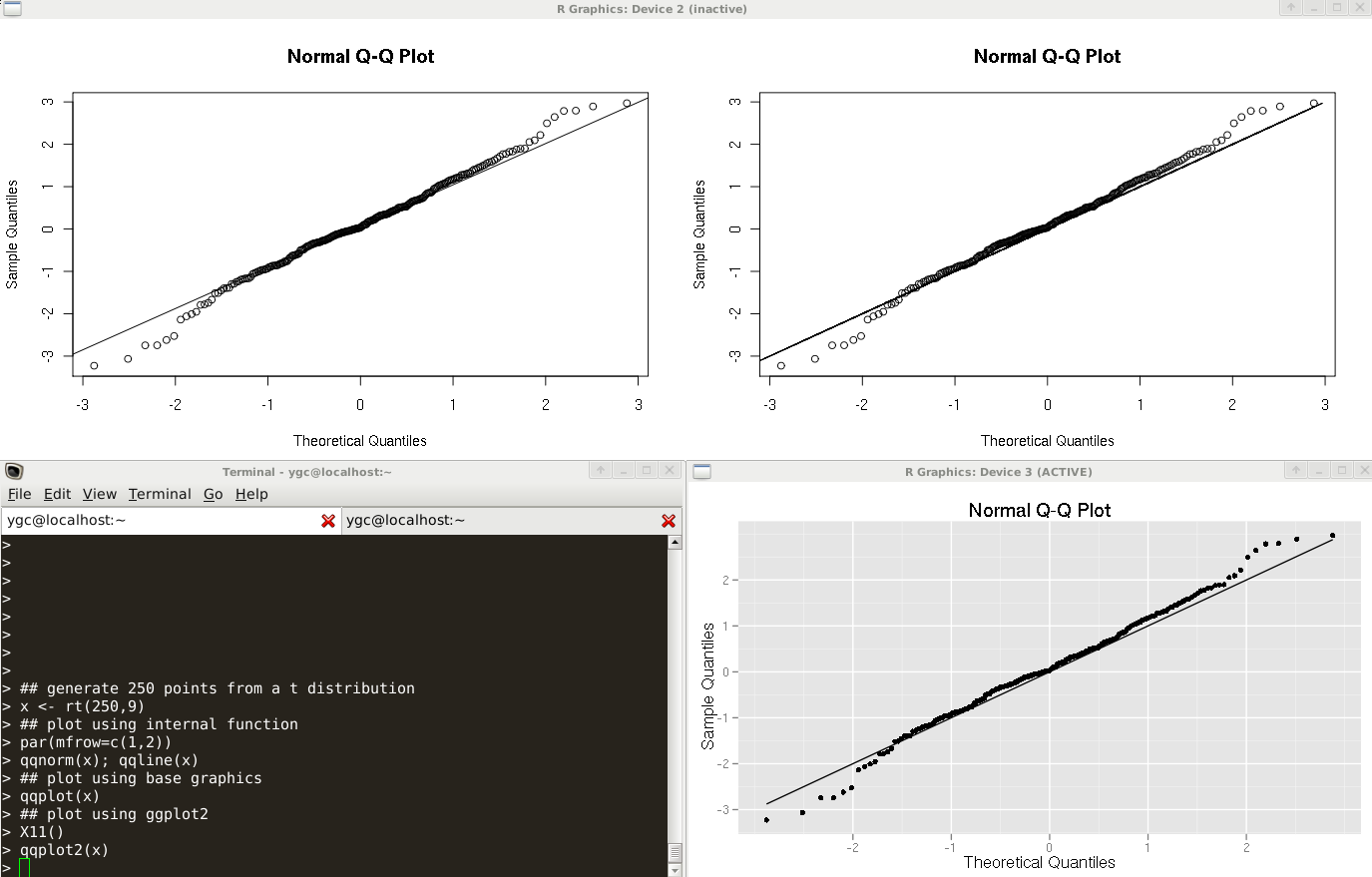
QQ plot

虽然R提供了很多作图函数，但自己实现一下，是非常好的体验，而且能够让我们了解其中的细节。

最近在读＜Modern Applied Statistics With S-PLUS＞，115页讲到Q-Q图时，书中给出了一个Trellis的实现。（Trellis是S/S-PLUS的可视化系统，在R里的对等实现是lattice包）。

我们知道一组数字，可以算4分位数，分别是25%， 50%（中位数）， 75%，它等于该组数字中所有数值由小到大排列后第X%的数字，事实上每个数字都可以对应一个X%，Q-Q图很简单，把样本数据和理论分布算出来的quantiles，画个散点图而已。分别用base graph和ggplot2实现，图中三个图分别由系统函数qqnorm，和这里定义的qqplot, qqplot2画出来。

qqplot <- function(y, distribution=qnorm) {
  x <- distribution(ppoints(y))
  plot(x, sort(y),
       xlab="Theoretical Quantiles",
       ylab="Sample Quantiles",
       main="Normal Q-Q Plot"
       )
  lines(y,y)
}

qqplot2 <- function(y, distribution=qnorm) {
  require(ggplot2)
  x <- distribution(ppoints(y))
  d <- data.frame(x=x, y=sort(y))
  p <- ggplot(d, aes(x=x, y=y)) +
    geom_point() +
      geom_line(aes(x=x, y=x)) +
        ggtitle(title="Normal Q-Q Plot") +
          xlab("Theoretical Quantiles") +
            ylab("Sample Quantiles")
  return(p)
}