Monte Carlo估计pi值

圆和外接正方形的面积比,是$ \frac{\pi r^2}{(2r)^2} = \frac{\pi}{4}$.
通过这一比值,可以使用蒙特-卡罗方法来估计Pi,这是Monte Carlo方法的最经典的一个例子。
getPI <- function(N) {
x <- runif(N)
y <- runif(N)
hits <- sum(sqrt(x^2+y^2) < 1)
pi <- 4*hits/N
return(pi)
}
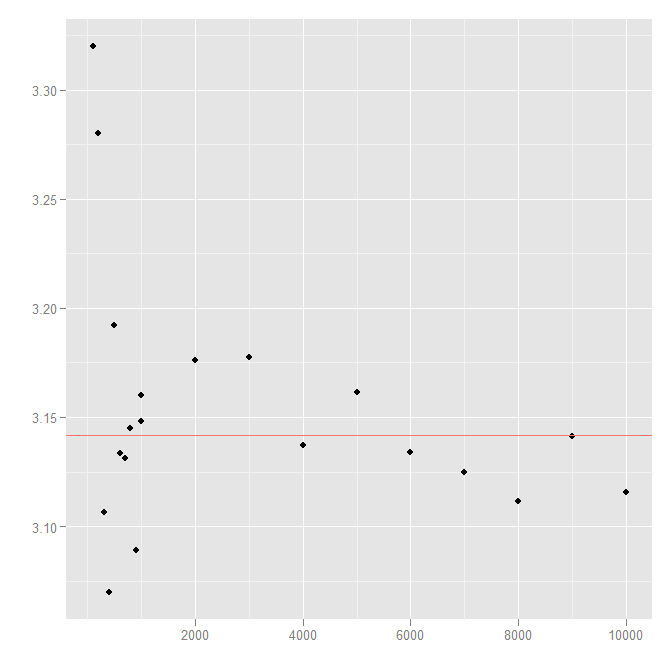
options(digits=15)
set.seed(12345)
n <- c(seq(from=100, to=1000, by=100),
seq(from=1000, to=10000, by=1000)
)
require(ggplot2)
p <- ggplot() +
aes(x=n, y=sapply(n, getPI)) +
geom_point() +
geom_hline(aes(yintercept=pi, colour="red")) +
xlab("")+ ylab("") +
theme(legend.position="none")
print(p)