用中值定理求根
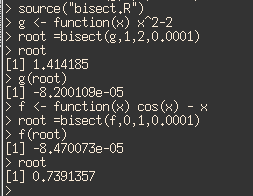
翻看了以前写的使用Newton-Raphson Method求一个数的开方,想到其实也可以用中值定理来实现。 中值定理:f(x)是一个连续性的函数,在[u,v]区间内,当c的值位于f(u)和f(v)之间时,至少存在一个点,满足f(x) = c 当f(u)和f(v)一正一负时,那么在[u,v]之间至少有一个根的存在,这个定理本来就是拿来证明根的存在的,但是其实也可以用来求解根。
把[u,v]的区间不断地缩小,就可以不断地逼近根的值,这不是人干的,但是适合计算机干,理论上,进行无穷次之后,便是根的准确值。当然不可能写个死循环,给定一个精度,当求解的根与实际值相差在精度范围内便退出循环,返回结果。 随手写了一段,可以拿来求根,就可以设计函数来求解无理数的有理数近似值,可以求解函数值等于某一值的x值,可以求解两个函数的交点等等。
bisect <- function(f, u, v, eps){
if ( f(u) * f(v) > 0)
stop (" error, select another value for u or v...")
if ( f(u) < 0) {
u1 <- u
v1 <- v
} else {
u1 <- v
v1 <- u
}
cnt <- 1
step <- log2(abs(u1-v1)/eps)
while ( cnt < step ){
m <- (u1+v1)/2
if ( f(m) == 0)
break
if ( f(m) < 0 ) {
u1 <- m
} else {
v1 <- m
}
cnt <- cnt + 1
}
return (m)
}