递归正如‘盗梦空间’中的场景：

PS: 使用《windows用户, 截屏新手段》可以一句for循环生成类似这种效果的图。

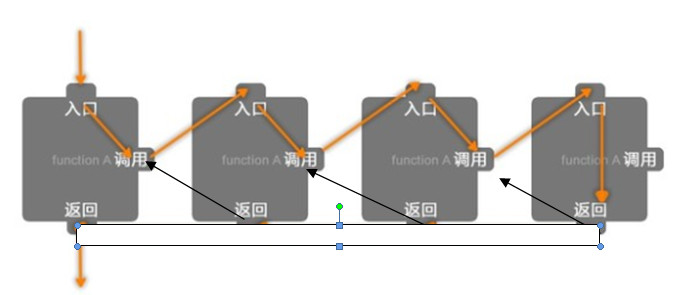
简言之就是不断调用自己，

经常我们会拿fibonacci数来讲解递归，正如在Rabbits and Recurrence Relations一题中所实现的，我使用了静态变量来缓存，以加快运行速度。R版本的实现可以参考tricky things in R一文，相对应于C的静态变量，在R中使用了局部的全局变量，这需要用<<-来赋值。

在开发ggtree时，unrooted layout最早的版本就是使用递归实现，但BiocCheck会把<<-报出来，而Bioconductor的人不喜欢看到这个赋值符，于是我改成了现在的版本，使用for loop。递归和循环一样，都只是程序的一种控制机制，某些递归实现代码非常短的同时，可读性非常强。

Example 1

比如我们要写writeSequence这样的函数：

Call                    Output
writeSequence(1);   1
writeSequence(2);   1 1
writeSequence(3);   2 1 2
writeSequence(4);   2 1 1 2
writeSequence(5);   3 2 1 2 3
writeSequence(6);   3 2 1 1 2 3

public void writeSequence(int n) {
    if (n < 1)
    throw new IllegalArgumentException();

    if (n == 1) {
    System.out.print(1);
    return;
    }

    if (n == 2) {
    System.out.print("1 1");
    return;
    }

    int x = (int) Math.ceil(n/2.0);
    
    System.out.print(x + " ");
    writeSequence(n-2);
    System.out.print(" " + x);
}

Continue reading

Monte Carlo方法由冯·诺伊曼于二战时提出，1777年法国人布丰用此思路估计pi值被认为是Monte Carlo的起源，这个方法简单又快速，通过产生随机数，将数值计算问题变成随机变量的某些特征值（比如期望值）。

积分运算，和估计pi值一样，用hit and miss法估计。

hit_miss <- function(fun, lower, upper, n=500) {
    # Monte Carlo integration using the hit and miss method
    x <- runif(n, lower, upper)
    f.value <- sapply(seq(lower, upper, 0.001), fun)
    f.min <- min(f.value)
    f.max <- max(f.value)
    y <- runif(n, f.min, f.max)
    hits <- sum(y <= fun(x))
    area <- (upper-lower) * f.min + hits/n * (upper-lower) * (f.max-f.min)
    return(area)
}

hit and miss方法收敛太慢，效率并不高，通常所说的MC积分是指下面这个方法。

Continue reading

圆和外接正方形的面积比，是$ \frac{\pi r^2}{(2r)^2} = \frac{\pi}{4}$.

通过这一比值，可以使用蒙特-卡罗方法来估计Pi，这是Monte Carlo方法的最经典的一个例子。

getPI <- function(N) {
    x <- runif(N)
    y <- runif(N)
    hits <- sum(sqrt(x^2+y^2) < 1)
    pi <- 4*hits/N
    return(pi)
}

Continue reading

Continue reading

Numerical root finding methods use iteration, producing a sequence of numbers that hopefully converge towards a limits which is a root. This post only focuses four basic algorithms on root finding, and covers bisection method, fixed point method, Newton-Raphson method, and secant method.

The simplest root finding algorithms is the bisection method. It works when f is a continuous function and it requires previous knowledge of two initial gueeses, u and v, such that f(u) and f(v) have opposite signs. This method is reliable, but converges slowly. For detail, see https://guangchuangyu.github.io/cn/2008/11/bisect-to-solve-equation/ .

Root finding can be reduced to the problem of finding fixed points of the function g(x) = c*f(x) +x, where c is a non-zero constant. It is clearly that f(a) = 0 if and only if g(a) = a. This is the so called fixed point algorithm.

Continue reading

R currently supports two internal OOP systems (S3 and S4), and several others as add-on packages, such as R.oo, and OOP.

S3 is easy to use but not reliable enough for large software projects. The S3 system emphasize on generic functions and polymorphism. It’s a function centric system which is different from class centric system like JAVA.

Continue reading

写给某个小朋友看，希望我的一点看法，能有用。欢迎讨论。。

为什么会有编程语言？

计算机史前有过不同的理论，但最后活下来的，只有图灵机一个模型。现在的计算机，都是基于此发展的，跟二战前那个三层楼高的计算机，没啥区别，那个机器一堆开关，人工操作。CPU做的计算也是开关的逻辑计算。所以计算机的语言是01二进制，一开一关，告诉计算机要不要发出电子脉冲。写一个程序全是01数字组成的，对于人来说是mission impossible！所以必须要有编程语言。编程语言就是为了抽象计算机机械原理的一面。

LOAD A ADD B STORE C

实现两个数的加和，这是人类可读的语言，而不是一串01所组成的不可读的机器语言。

抽象是最关键的。所有的编程语言都是为了实现抽象。越是高级的语言，抽象度越高，抽象度越高越好！

Continue reading