根号2的几何作图

读研时买了很多书，大部分都没时间看，《什么是数学》就是其中的一本。 这两天翻看了一点。

《第二章：数学中的数系》讲到了当年的伟大发现，一个正方形的对角线与它的边是不可公度的。而由不可公度线段，引入的无理数概念，引入负数，在17世纪都是个另人不安的事情，无理数是个巨大的飞跃，

73页中的图10,给出了 $\sqrt{2}$的几何作图。

我用R尝试把它画出来：

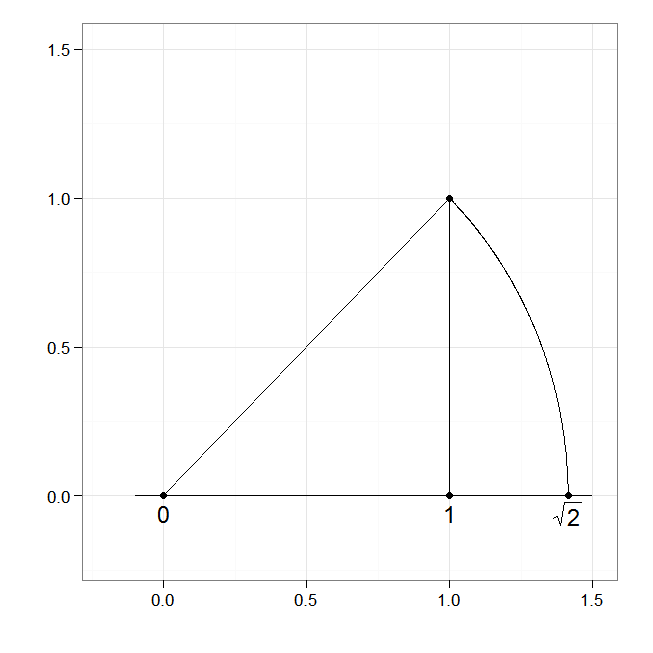
dd <- data.frame(x=c(0,1,1,0), y=c(0,0,1,0))
pp <- ggplot(dd,aes(x,y))
pp <- pp +
    geom_point() + 
    geom_path() +
    xlim(-0.2,1.5) +
    ylim(-0.2,1.5)

xc <- seq(1, sqrt(2), 0.001)
yc <- sqrt(2-xc^2)
xc <- c(xc,sqrt(2))
yc <- c(yc,0)
d2 <- data.frame(x = xc, y = yc)

pp <- pp + 
    geom_path(data=d2) + 
    annotate("line", x=c(-0.1,1.5),y=c(0,0)) + 
    geom_point(aes(x=sqrt(2),y=0)) +
    annotate("text",
            x=c(0, 1, sqrt(2)), 
            y =c(-0.06, -0.06, -0.06), 
            label=c(0, 1, as.character(expression(sqrt(2)))), 
            parse=TRUE) + 
    xlab("") + 
    ylab("") + 
    theme_bw() 

print(pp)

$\sqrt{2}$ 的有理数近似值可以通过Newton-Raphson法求得。